windpowerlib.power_output.power_curve_density_correction¶
- windpowerlib.power_output.power_curve_density_correction(wind_speed, power_curve_wind_speeds, power_curve_values, density)[source]¶
Calculates the turbine power output using a density corrected power curve. This function is carried out when the parameter density_correction of an instance of the
ModelChainclass is True.- Parameters:
wind_speed (pandas.Series or numpy.array) – Wind speed at hub height in m/s.
power_curve_wind_speeds (pandas.Series or numpy.array) – Wind speeds in m/s for which the power curve values are provided in power_curve_values.
power_curve_values (pandas.Series or numpy.array) – Power curve values corresponding to wind speeds in power_curve_wind_speeds.
density (pandas.Series or numpy.array) – Density of air at hub height in kg/m³.
- Returns:
Electrical power output of the wind turbine in W. Data type depends on type of wind_speed.
- Return type:
pandas.Series or numpy.array
Notes
The following equation is used for the site specific power curve wind speeds [1] [2] [3]:
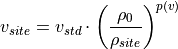
- with:
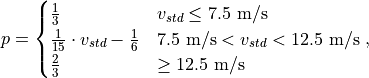
v: wind speed [m/s],
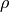 : density [kg/m³]
: density [kg/m³]
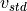 is the standard wind speed in the power curve
(
is the standard wind speed in the power curve
(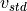 ,
, 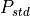 ),
),
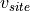 is the density corrected wind speed for the power curve
(
is the density corrected wind speed for the power curve
(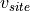 ,
, 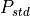 ),
),
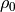 is the ambient density (1.225 kg/m³)
and
is the ambient density (1.225 kg/m³)
and 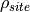 the density at site conditions (and hub height).
It is assumed that the power output for wind speeds above the maximum
and below the minimum wind speed given in the power curve is zero.
the density at site conditions (and hub height).
It is assumed that the power output for wind speeds above the maximum
and below the minimum wind speed given in the power curve is zero.References