windpowerlib.power_curves.smooth_power_curve

windpowerlib.power_curves.smooth_power_curve(power_curve_wind_speeds, power_curve_values, block_width=0.5, wind_speed_range=15.0, standard_deviation_method='turbulence_intensity', mean_gauss=0, **kwargs)[source]

Smoothes a power curve by using a Gauss distribution.

The smoothing serves for taking the distribution of wind speeds over space into account.

Parameters:

  • power_curve_wind_speeds (pandas.Series or numpy.array) – Wind speeds in m/s for which the power curve values are provided in power_curve_values.

  • power_curve_values (pandas.Series or numpy.array) – Power curve values corresponding to wind speeds in power_curve_wind_speeds.

  • block_width (float) – Width between the wind speeds in the sum of equation (1). Default: 0.5.

  • wind_speed_range (float) – The sum in the equation below is taken for this wind speed range below and above the power curve wind speed. Default: 15.0.

  • standard_deviation_method (str) – Method for calculating the standard deviation for the Gauss distribution. Options: ‘turbulence_intensity’, ‘Staffell_Pfenninger’. Default: ‘turbulence_intensity’.

  • mean_gauss (float) – Mean of the Gauss distribution in gauss_distribution(). Default: 0.

  • intensity (turbulence) – Turbulence intensity at hub height of the wind turbine, wind farm or wind turbine cluster the power curve is smoothed for.

Returns:

Smoothed power curve. DataFrame has ‘wind_speed’ and ‘value’ columns with wind speeds in m/s and the corresponding power curve value in W.

Return type:

pandas.DataFrame

Notes

The following equation is used to calculated the power curves values of the smoothed power curve [1]:

(1)P_{smoothed}(v_{std})=\sum\limits_{v_i} \Delta v_i \cdot P(v_i) \cdot \frac{1}{\sigma \sqrt{2 \pi}} \exp \left[-\frac{(v_{std} - v_i -\mu)^2}{2 \sigma^2} \right]

with:

P: power [W], v: wind speed [m/s], 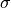\sigma: standard deviation (Gauss), 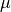\mu: mean (Gauss)

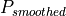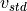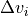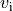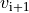
P_{smoothed} is the smoothed power curve value, v_{std} is the standard wind speed in the power curve, \Delta v_i is the interval length between v_\text{i} and v_\text{i+1}

Power curve smoothing is applied to take account of the spatial distribution of wind speed. This way of smoothing power curves is also used in [2] and [3].

The standard deviation 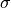\sigma of the above equation can be calculated by the following methods.

‘turbulence_intensity’ [2]:

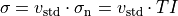
\sigma=v_\text{std} \cdot \sigma_\text{n}=v_\text{std} \cdot TI

with:

TI: turbulence intensity

‘Staffell_Pfenninger’ [4]:

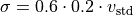
\sigma=0.6 \cdot 0.2 \cdot v_\text{std}

References